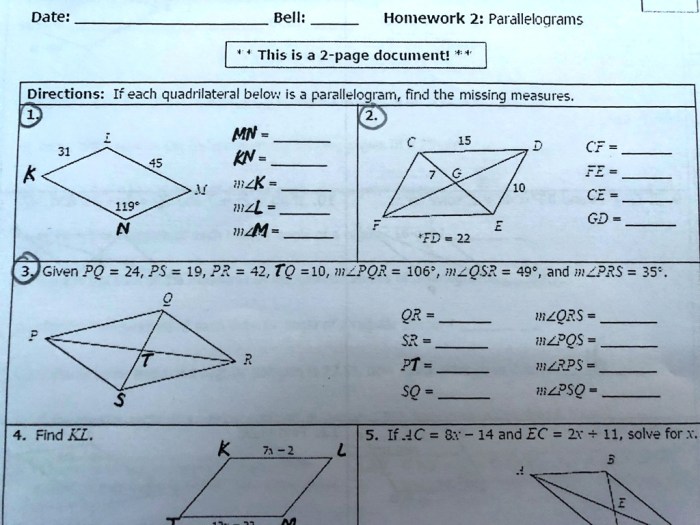
Unit 8 polygons and quadrilaterals homework 2 parallelograms – Unit 8 Polygons and Quadrilaterals Homework 2: Parallelograms delves into the captivating world of these fascinating shapes, unveiling their unique characteristics and practical applications. From the fundamental properties that define parallelograms to the diverse types that exist, this exploration promises to illuminate the significance of these geometric wonders.
Parallelograms, with their parallel opposite sides and congruent angles, form the cornerstone of this study. We will delve into the nuances of squares, rectangles, rhombuses, and rhomboids, unraveling the distinct features that set them apart. Through a comprehensive comparison table, we will establish a clear understanding of their similarities and differences.
Definition of Parallelograms
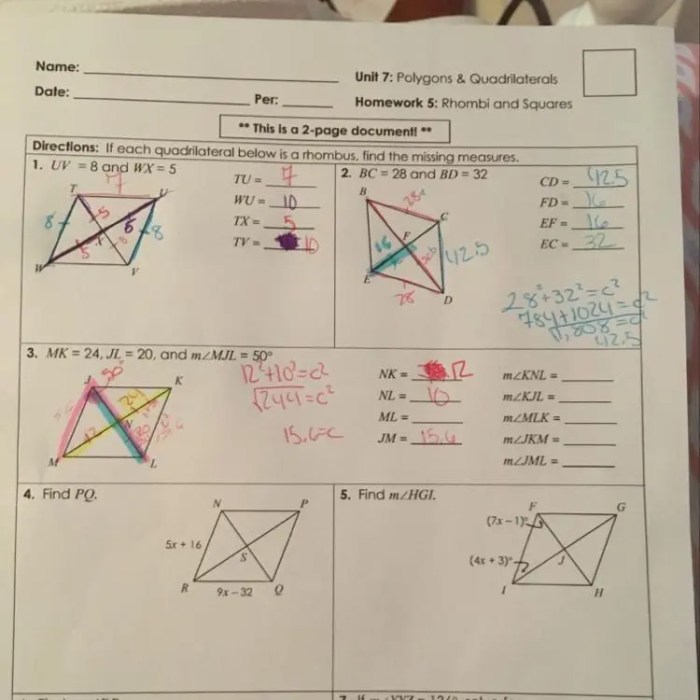
A parallelogram is a quadrilateral that has opposite sides parallel and congruent. This means that the opposite sides of a parallelogram are equal in length and run in the same direction. Parallelograms have two pairs of parallel sides and two pairs of congruent sides.
Some key characteristics of parallelograms include:
- Opposite sides are parallel and congruent.
- Opposite angles are congruent.
- Diagonals bisect each other.
- The sum of the interior angles is 360 degrees.
Parallelograms are common in everyday life. Some examples of real-world objects that are parallelograms include:
- Rectangles
- Squares
- Rhombuses
- Rhomboids
Types of Parallelograms
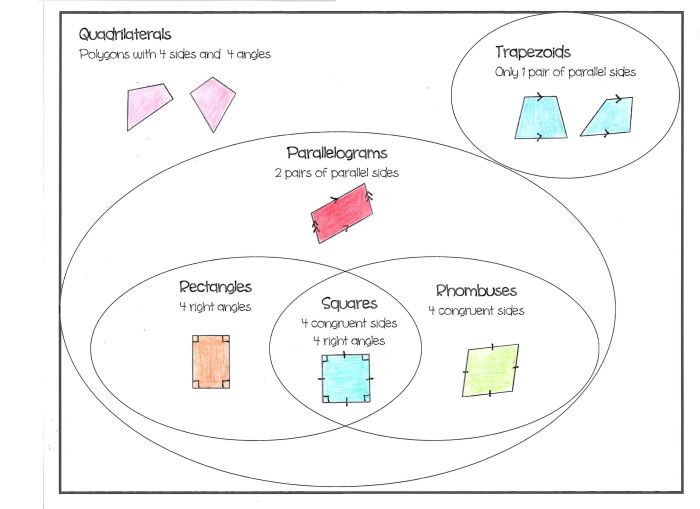
There are four main types of parallelograms:
- Rectangles: Rectangles have four right angles and opposite sides are parallel and congruent.
- Squares: Squares are rectangles with all four sides equal in length.
- Rhombuses: Rhombuses have four congruent sides and opposite angles are congruent.
- Rhomboids: Rhomboids have opposite sides parallel and congruent, but their angles are not necessarily right angles.
Properties of Parallelograms
Parallelograms have a number of geometric and algebraic properties. Some of the most important properties of parallelograms include:
- Diagonals bisect each other: The diagonals of a parallelogram bisect each other, meaning they divide each other into two equal parts.
- Opposite angles are congruent: The opposite angles of a parallelogram are congruent, meaning they have the same measure.
- Area formula: The area of a parallelogram is equal to the product of its base and height.
- Perimeter formula: The perimeter of a parallelogram is equal to the sum of the lengths of its four sides.
Applications of Parallelograms: Unit 8 Polygons And Quadrilaterals Homework 2 Parallelograms
Parallelograms have a wide range of applications in various fields, including architecture, engineering, and design. Some of the most common applications of parallelograms include:
- Architecture: Parallelograms are often used in the design of buildings and other structures. For example, the base of a pyramid is a parallelogram.
- Engineering: Parallelograms are used in the design of bridges, trusses, and other structures. For example, the trusses in a bridge are often parallelograms.
- Design: Parallelograms are used in the design of furniture, textiles, and other products. For example, the seat of a chair is often a parallelogram.
Question Bank
What are the key characteristics of parallelograms?
Parallelograms are quadrilaterals with opposite sides parallel and congruent, and opposite angles congruent.
What are the different types of parallelograms?
The different types of parallelograms include squares, rectangles, rhombuses, and rhomboids.
What are the practical applications of parallelograms?
Parallelograms find applications in architecture, engineering, and design due to their inherent properties.