Graphs of square root functions worksheet – Embark on an illuminating journey into the realm of square root functions and their captivating graphs. This comprehensive worksheet delves into the fundamental concepts, properties, and applications of these mathematical marvels, equipping you with a profound understanding that transcends mere textbook knowledge.
Unravel the secrets of square root functions, uncovering their unique characteristics and the intriguing patterns they exhibit on the coordinate plane. Prepare to be captivated as we explore the practical significance of these functions in diverse fields, ranging from physics to economics.
Introduction
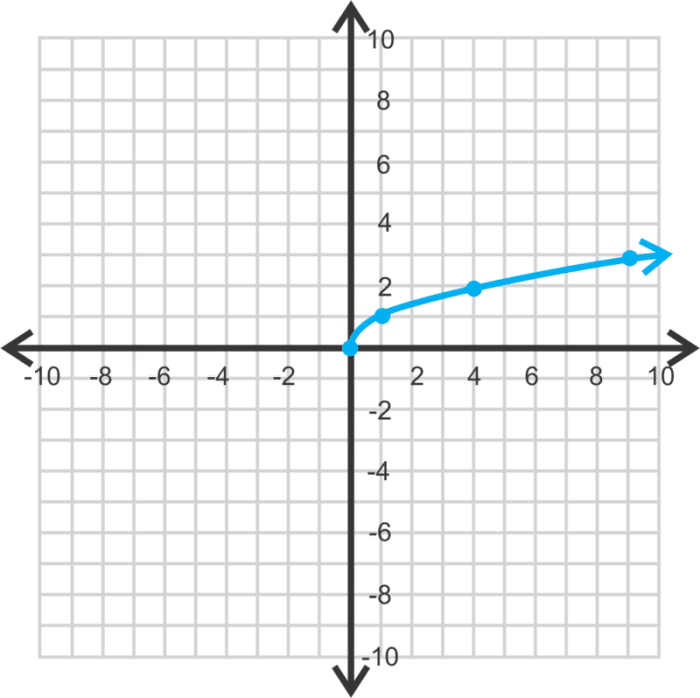
Square root functions are mathematical expressions that involve the square root of a variable. They are important in various fields, such as physics, engineering, and economics, and understanding their graphs is crucial for analyzing and solving problems.
Properties of Square Root Functions
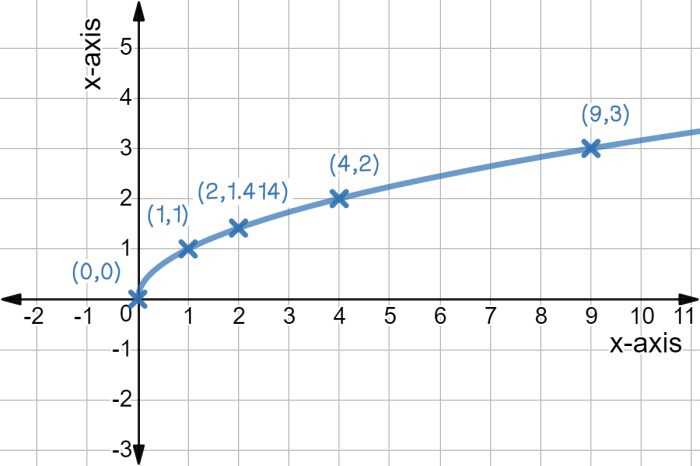
Square root functions have several key properties:
- Domain: The domain of a square root function is all non-negative real numbers (x ≥ 0).
- Range: The range of a square root function is all non-negative real numbers (y ≥ 0).
- Symmetry: Square root functions are symmetric about the y-axis.
Graphing Square Root Functions: Graphs Of Square Root Functions Worksheet
To graph a square root function, follow these steps:
- Plot the vertex at (0, 0).
- Move up and to the right along the y-axis to plot additional points.
- Reflect the points across the y-axis to create the left-hand side of the graph.
Transformations can be applied to shift, stretch, or shrink the graph.
Applications of Square Root Functions
Square root functions have numerous real-world applications, including:
- Calculating the distance between two points.
- Determining the speed of an object.
- Solving equations in physics and engineering.
- Modeling population growth and decay.
Top FAQs
What are the key properties of square root functions?
Square root functions possess distinctive properties, including a restricted domain, a non-negative range, and a characteristic V-shape graph that exhibits symmetry about the y-axis.
How can I graph square root functions effectively?
Mastering the art of graphing square root functions involves understanding their properties and utilizing transformations, such as translations and reflections, to accurately plot their curves on the coordinate plane.
What are some real-world applications of square root functions?
Square root functions find practical applications in numerous fields, including physics (projectile motion), engineering (stress analysis), and economics (demand curves), demonstrating their versatility and significance in the real world.